Tree Data Structure- Types, Operations, Applications
The construction of a computer language requires a tree data structure. It provides actions like element addition, deletion, and searching. A non-linear data structure called a tree helps in organizing a data hierarchy.

Have you made a family tree in one of those school assignments when you were a kid?
Even if you haven't, you must have seen one.
It basically starts from a root point (grandparents or maybe even great grandparents) and then spreads across multiple generations in a hierarchical order.
If you still can't picture it, just imagine an inverted tree (literally, a tree). It originates from the root and then several branches come out at different heights.
That's what a tree data structure looks like.
We've learned the linear data structures like arrays, stacks, queues, and linked lists in our previous articles. (If you haven't, please refer to this list)
Table of Contents:
Tree data structure terminology
What is a tree data structure?
Now, we're going to learn about a non-linear data structure - Tree.
A tree is a hierarchical data structure that contains a collection of nodes connected via edges so that each node has a value and a list of pointers to other nodes. (Similar to how parents have the reference to their children in a family tree)
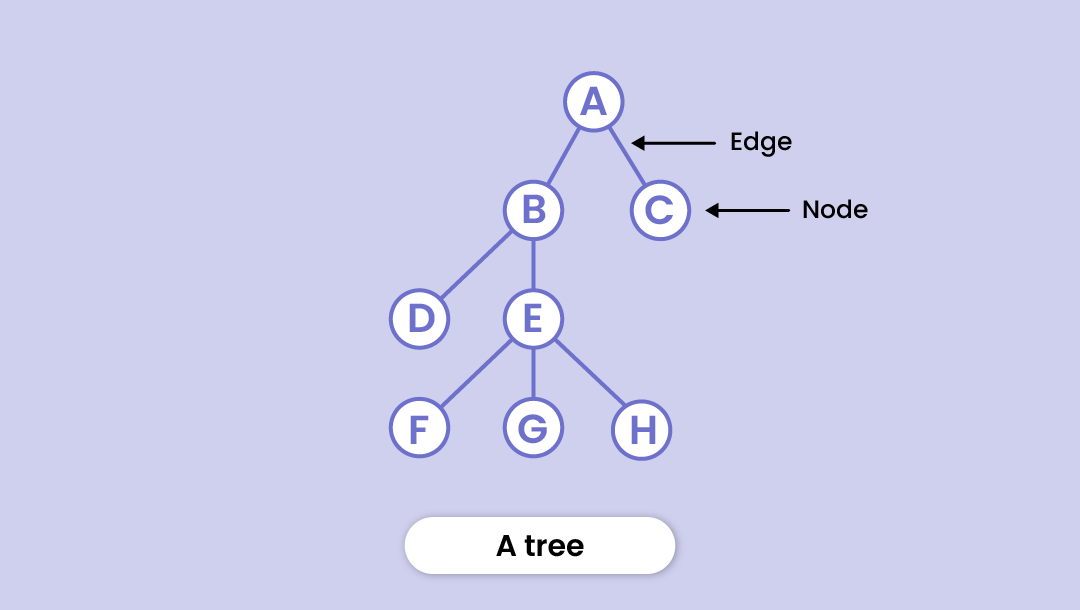
Following are the key points of a tree data structure:
- Trees are specialized to represent a hierarchy of data
- Trees can contain any type of data be it strings or numbers
Here’s the logical representation of a tree:
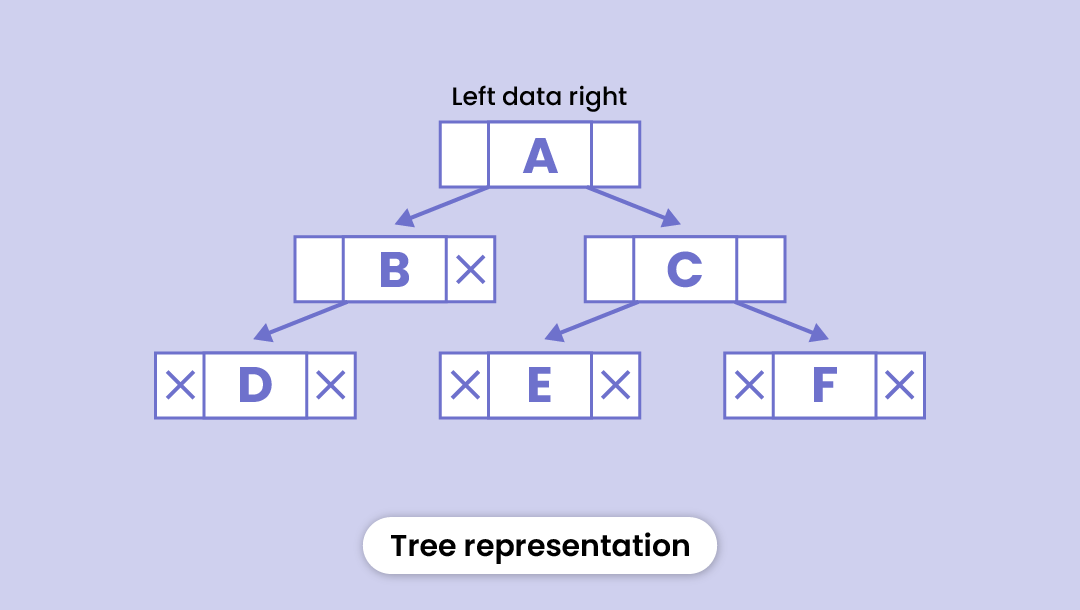
Basic terms of a tree data structure
Root node
The topmost node in the tree hierarchy is known as the root node. In other words, it's the origin point of the tree that doesn't have any parent node.
Child node
The descendant of any node is said to be a child node.
Parent node
If the node has a descendant i.e. a sub-node, it's called the parent of that sub-node.
Siblings
Just like a family tree, nodes having the same parent node are called siblings.
Leaf node
It's the bottom-most node in the tree that doesn't have any child node. They are also called external nodes. The "end" of a tree branch is normally where the leaf nodes are located.
Internal node
A node having at least one child node is known as an internal node. Internal nodes in a tree structure are often located "between" other nodes.
Ancestor Node
Any node that lies between the root and the current node is considered to be an ancestor node. You may think of ancestor nodes as "parents, grandparents, etc."
Descendant
A descendant is any child, grandchild, great-grandchild, etc. of the current node. Any node in the tree structure that is "below" the current node is referred to as a descendent.
Edges
The link between any two nodes is called an edge.
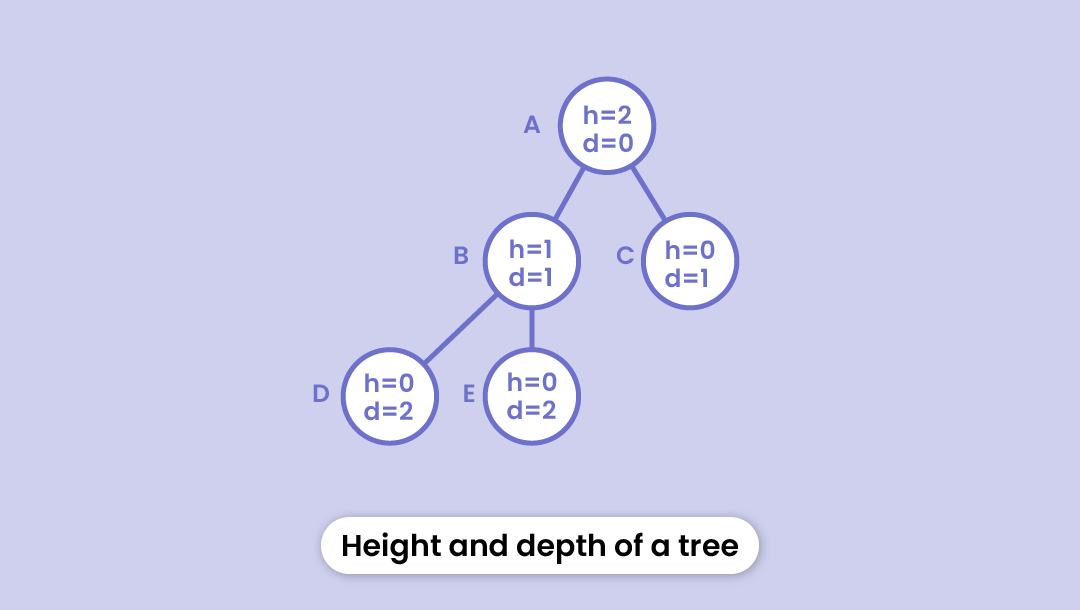
Height
The height of a node is the number of edges from that node to the leaf node (the lowermost node in the hierarchy)
In the figure below - the height of node B will be the number of edges from B to the external node i.e. D. Thus h = 1)
Depth
The depth of a node is the number of edges it takes from the root node to that particular node.
In the figure below - the depth of node D will be the number of edges from A to D. Thus d = 2)
Degree
The total number of branches coming out of a node is considered to be the degree of that node.
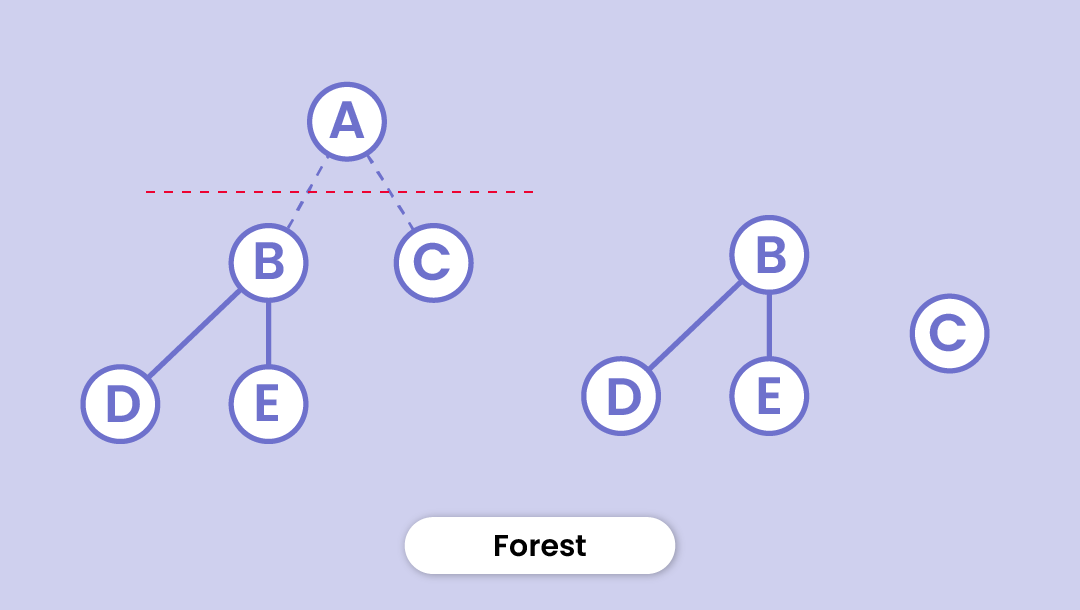
Forest
It's not hard to guess, is it? A collection of disconnected trees is called a forest. If you cut the root of a tree, the disjoint trees hence formed make up a forest. (As shown in the figure)
The characteristics of tree data structures
A tree, which replicates a hierarchical tree structure with a collection of connected nodes, is a common data structure in computer science. The following characteristics of a tree data structure:
- Number of edges
- Recursive data structure
- Height of node x
- Depth of node x
Continue reading to understand more about each of these tree data structure's characteristics in greater depth.
Number of edges: A tree's edge count is always one less than its node count. The reason for this is that on any path from the root to any leaf node, there is always one less edge than there are nodes.
Recursive data structure: When a tree comprises a root node and nodes that have zero or more children each, a tree is a recursive data structure. The tree's offspring nodes are situated below the root node, which is the uppermost node. The term "n-aryl tree" refers to a tree whose nodes each have one or more children.
Height of node x: The distance along the longest route leading from a node to any leaf node is used to measure a node's height. To put it another way, it is just the quantity of edges along the route leading from that leaf node to the deepest leaf node.
Depth of node x: The distance along the shortest route from the root to a node is referred to as the node's depth. In other words, it only refers to how many edges there are on the route leading from the root to that specific node.
Types of Trees
Binary Tree
In this data structure, each parent node can contain a maximum of two children nodes. (The left and the right child)
Each node in a binary tree contains the following three parts:
- Data
- Pointer to the left child
- Pointer to the right child
In the image, Node B contains both the pointers (left and right child), whereas nodes C, D, and E are leaf nodes, so they contain null pointers.
There are four major types of binary trees:
Full Binary Tree - Every parent node has either two or no children.
Perfect Binary Tree - Every parent node has exactly two child nodes and all the external nodes (leaf nodes) are at the same level.
Complete Binary Tree - In this case, every level must be filled, and all the leaf elements lean towards the left.
Degenerate Tree - The tree in which the parent nodes have a single child, either left or right is called a degenerate tree.
Balanced Binary Tree - A binary tree in which the height difference between the left and the right child nodes is either 0 or 1.
Binary Search Tree
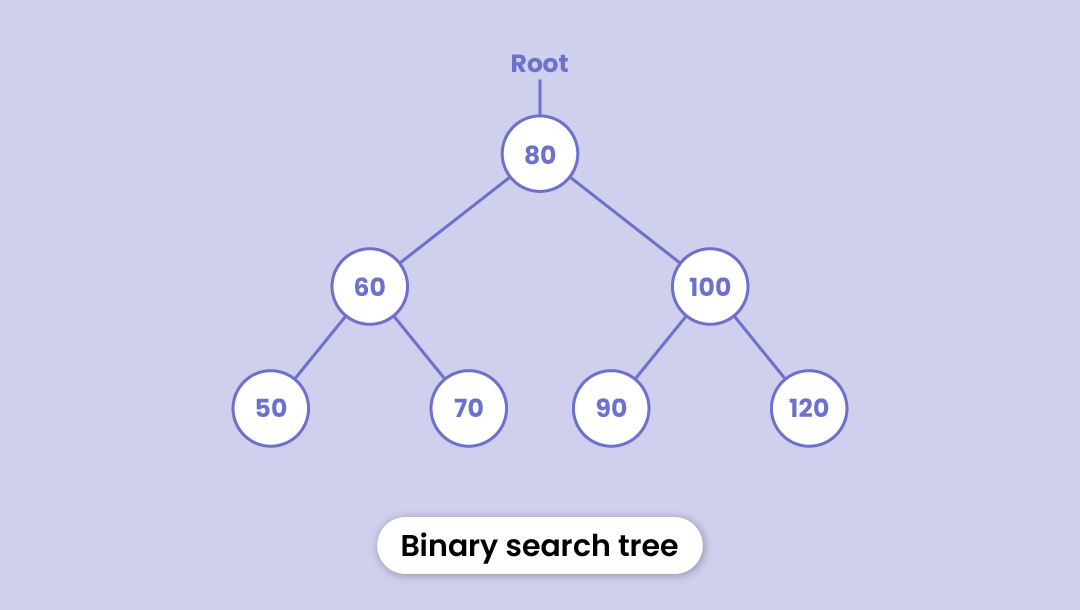
We've already learned about the binary tree.
A binary tree that maintains some order to arrange the nodes is called a binary search tree.
It is similar to a binary tree in the sense that each node can have at most two children; however, there are a few specifications:
- Each node of the left subtree has a smaller value than the root node
- Each node of the right subtree is larger than the root node
- This arrangement follows throughout the tree i.e. both subtrees of all the nodes have the same properties
The search operation is much easier in a binary search tree. If the required value is below the root, we only need to traverse the left subtree. Similarly, if the value is above the root, we can say that it's not in the left subtree and we only need to traverse the right trajectory.
Here's the search algorithm:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left)
If number > root->data
return search(root->right)AVL Tree
To understand AVL Tree, we first need to understand the term - Balance Factor.
The balance factor of a node is the difference between the height of the left subtree and the height of the right subtree of that particular node.
It can also be defined as a height-balanced binary search tree.
For a tree to be height balanced, the balance factor of each node must be between -1 to 1 (-1, 0, or 1).
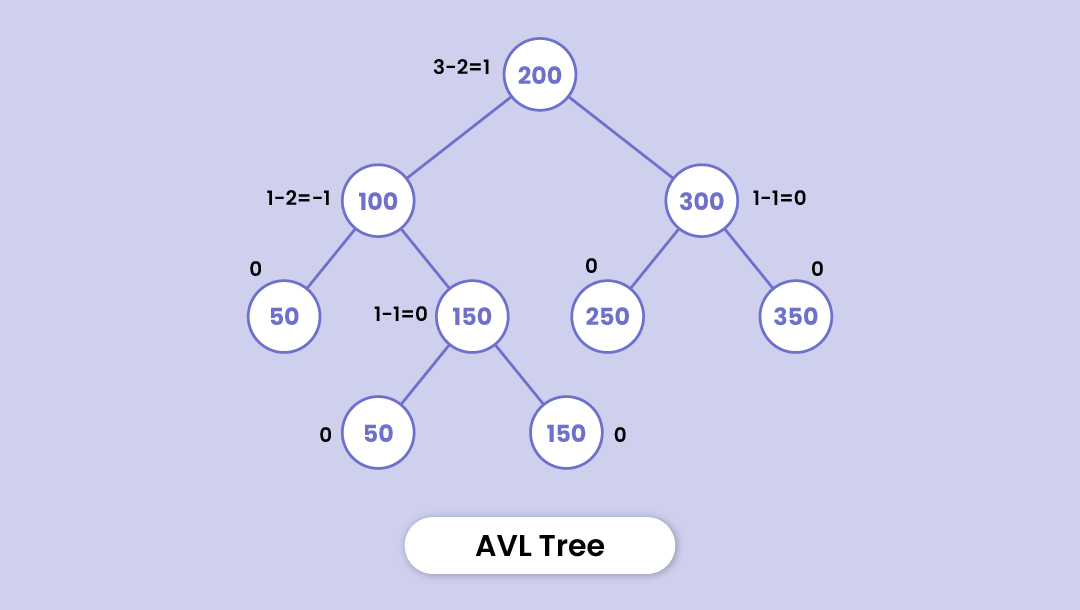
Let's understand through this example -
Here, node 200 has a balance factor of 1. How?
(Height of left child node 100 - the height of node 300)
Similarly, node 100 has a balance factor of -1; as the difference in the heights of its left subtree and the right subtree is -1.
AVL Tree allows the same search operation as a binary search tree as it follows the same properties. (Left subtree < root < right subtree )
B-Tree
It's a specialized self-balancing tree in which each node can have more than one key and more than two child nodes. It's also called a height-balanced m-way tree.
With its capacity to store multiple keys, a B-tree takes much lesser time to access physical storage media like a hard disk.
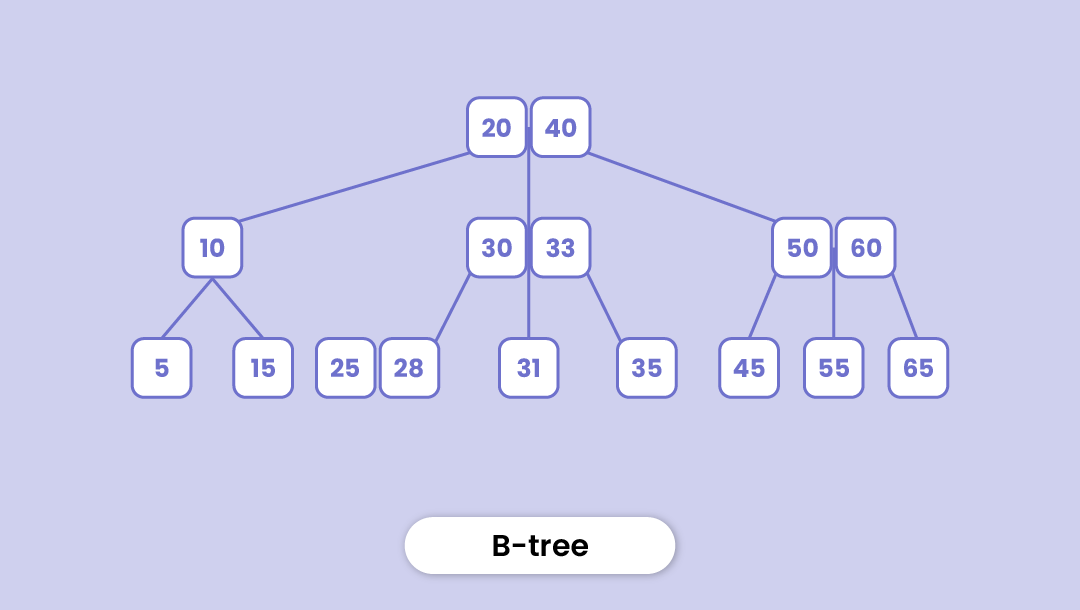
Since other tree types like binary search tree, AVL Tree, etc. can only contain one key in one node, storing a large number of keys increases their height by a stretch and the access time increases. B-tree solves this problem.
Here are a few properties of a B-tree:
- Each node in a B-Tree of 'm' order contains a maximum of 'm' children. Order in a B-tree represents the maximum number of children possible.
- The root nodes must contain at least 2 nodes
- All leaf nodes are at the same level (they have the same depth)
- If the tree is of x order, each internal node can contain at most x-1 keys with a pointer to every child.
Traversal in a tree data structure
In linear data structures like arrays, stacks, etc. there's only one way to traverse the data. But, a hierarchical data structure like a tree can have different ways of traversal.
In order to traverse a tree, we need to read all the nodes in the left subtree, the root node, and all the nodes in the right subtree.
There are mainly three ways of traversal depending on the order we want to follow:
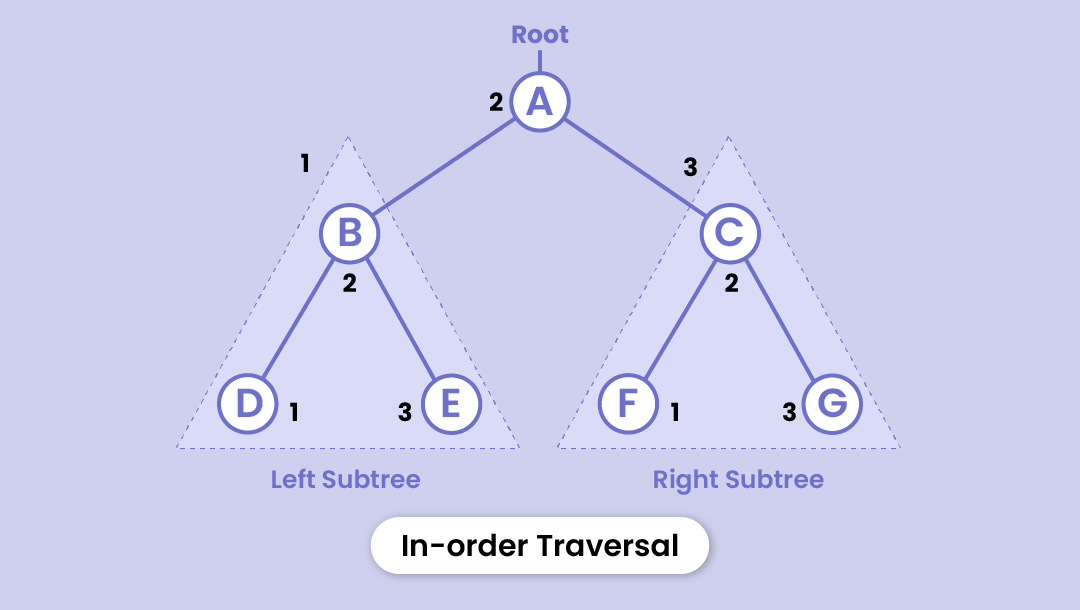
Inorder traversal
- It starts with visiting all the nodes in the left subtree
- Then visits the root node
- And finally, all the nodes in the right subtree are visited
Preorder traversal
- First, the root node is visited
- Then all the nodes in the left subtree
- And finally visits all the nodes in the right subtree
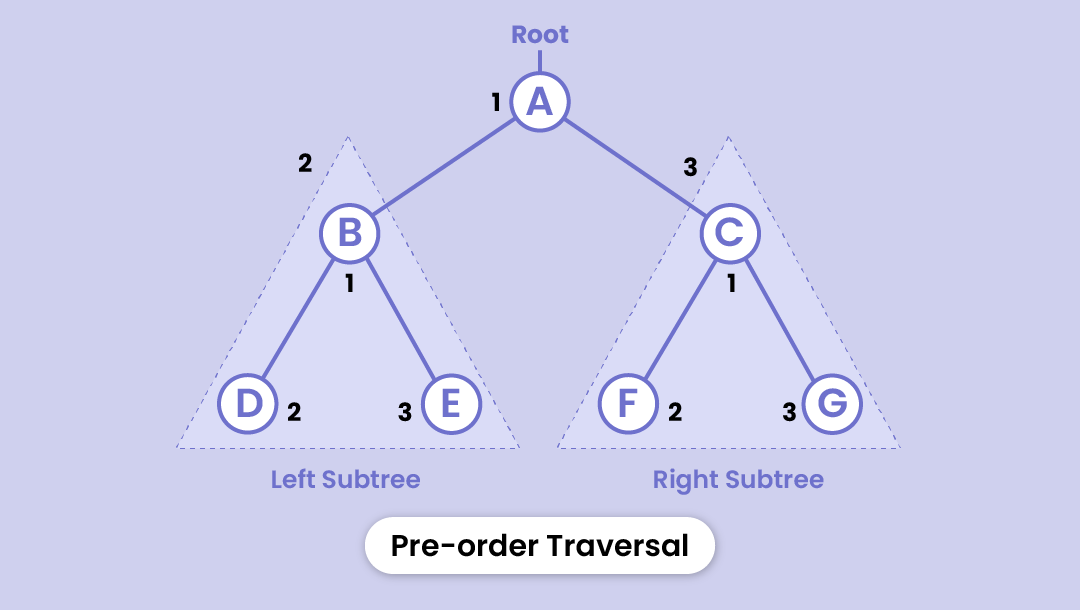
The order will be: A - B - D - E - C - F - G
Post-order traversal
- Starts with the nodes in the left subtree
- Visits the nodes in the right subtree
- And then visits the root node
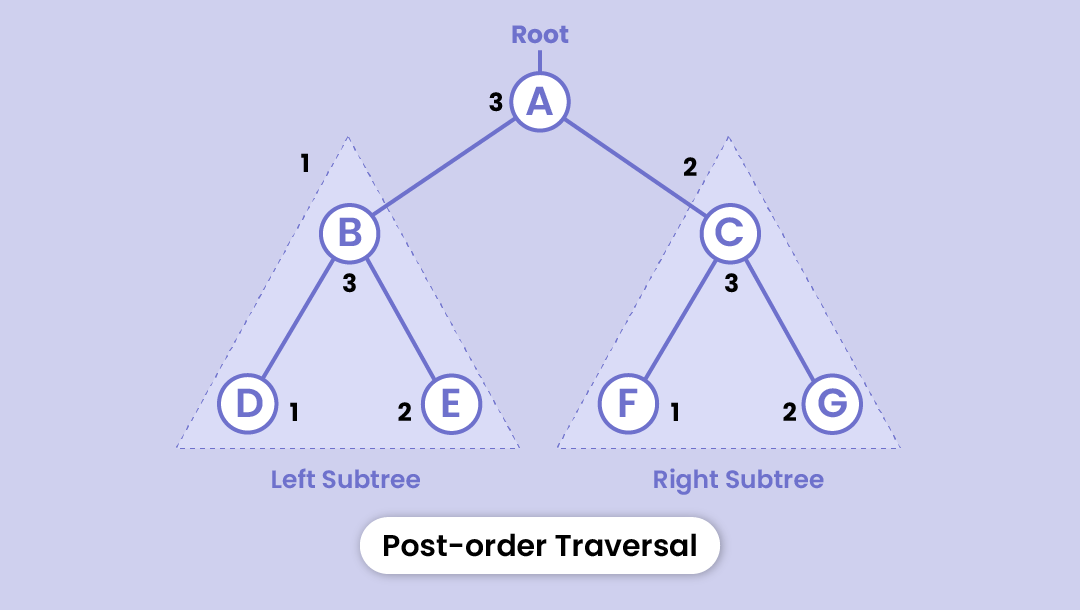
Here, the order will go as D - E - B - F - G - C - A
Basic operations of a tree
Here are a few basic operations you can perform on a tree:
Insertion
Insertion can be done in multiple ways depending on the location where the element is to be inserted.
- We can insert the new element at the rightmost or the leftmost vacant position
- Or just insert the element in the first vacant position we find when we traverse a tree
As we said there are many more ways we can insert a new element, but for this article's sake let's try the first method:
Let's determine the vacant place with In-order traversal.
Parameters: root, new_node
- Check the root if it's null, i.e., if it's an empty tree. If yes, return the new_node as root.
- If it’s not, start the inorder traversal of the tree
- Check for the existence of the left child. If it doesn't exist, the new_node will be made the left child, or else we'll proceed with the inorder traversal to find the vacant spot
- Check for the existence of the right child. If it doesn't exist, we'll make the right child as the new_node or else we'll continue with the inorder traversal of the right child.
Here’s the Pseudo-code to run this operation-
TreeNode insert_node_inorder(TreeNode root, TreeNode new_node)
{
if ( root == NULL )
return new_node
if ( root.left == NULL )
root.left = new_node
else
root.left = insert_node_inorder(root.left, new_node)
if ( root.right == NULL )
root.right = new_node
else
root.right = insert_node_inorder(root.right, new_node)
return root
}
Searching
It's a simple process in a binary tree. We just need to check if the current node's value matches the required value and keep repeating the same process to the left and right subtrees using a recursive algorithm until we find the match.
bool search(TreeNode root, int item)
{
if ( root == NULL )
return 0
if ( root.val == item )
return 1
if ( search(root.left, item) == 1 )
return 1
else if ( search(root.right, item) == 1 )
return 1
else
return 0
}
Deletion
It's a bit tricky process when it comes to the tree data structure. There are a few complications that come with deleting a node such as-
- If we delete a node, what happens to the left child and the right child?
- What if the node to be deleted is itself a leaf node?
Simplifying this - the purpose is to accept the root node of the tree and value item and return the root of the modified tree after we have deleted the node.
- Firstly, we'll check if the tree is empty i.e. the root is NULL. If yes, we'll simply return the root.
- We'll then search for an item in the left and the right subtree and recurse if found.
- If we don't find the item in both the subtrees, either the value is not in the tree or root.val == item.
- Now we need to delete the root node of the tree. It has three possible cases.
CASE 1 - The node to be deleted is a leaf node.
In this case, we'll simply delete the root and free the allocated space.
CASE 2 - It has only one child.
We can't delete the root directly as there's a child node attached to it. So, we'll replace the root with the child node.
CASE 3 - It has two children nodes.
In this case, we'll keep replacing the node to be deleted with its in-order successor recursively until it's placed on the leftmost leaf node. Then, we'll replace the node with NULL and delete the allocated space.
In other words, we'll replace the node to be deleted with the leftmost node of the tree and then delete the new leaf node.
This way, there's always a root at the top and the tree shrinks from the bottom.
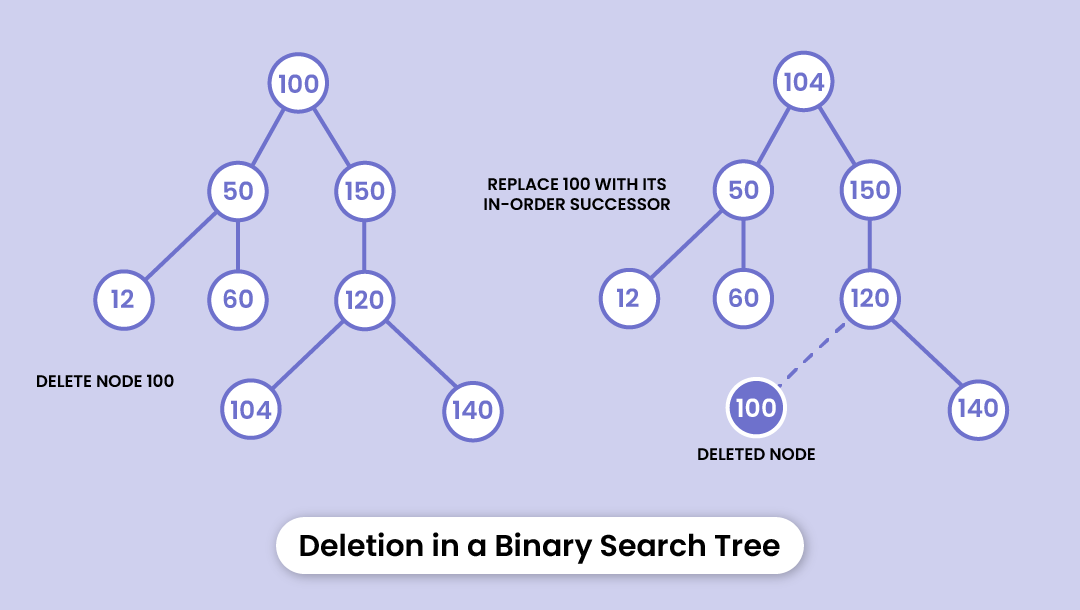
Here’s the pseudo-code to execute a deletion:
TreeNode delete_element(TreeNode root, int item)
{
if ( root == NULL )
return root
if ( search(root.left, item) == True )
root.left = delete_element(root.left, item)
else if ( search(root.right, item) == True )
root.right = delete_element(root.right, item)
else if ( root.val == item )
{
// No child exists
if ( root.left == NULL and root.right == NULL )
delete root
// Only one child exists
else if ( root.left == NULL or root.right == NULL )
{
if ( root.left == NULL )
return root.right
else
return root.left
}
// Both left and right child exists
else
{
TreeNode selected_node = root
while ( selected_node.left != NULL )
selected_node = selected_node.left
root.val = selected_node.val
root.left = delete_element(root.left, selected_node.val)
}
}
return root
}
Applications of Tree Data Structure
As we've mentioned above, tree data structure stores data in a hierarchical manner. Nodes are arranged at multiple levels. As with the file system on our computers, trees are also utilized to store data that naturally has hierarchical links. In addition, trees are utilized in the following applications.
- Information stored in the computer is in a hierarchical manner. There are drives that contain multiple folders. Each folder can have multiple subfolders. And then there are files like documents, images, etc.
- Searching for a node in a tree data structure (such as BST) is relatively faster, and so are other operations such as insertion and deletion, given its ordered structure.
- Trie is a type of tree data structure that is used to insert, search, and start strings. (Example - Contact list on your phone)
- We use a tree data structure to store data in routing tables in the routers.
- Programmers also use syntax trees in compilers to verify the syntax of the programs they write.
Final Thoughts
We hope you got the gist of the tree data structure. And it’s important to understand all data structures and algorithms if you want to become a top-notch programmer. DSA helps in building logic and problem-solving skills that are quite useful in real life too. (Here are 5 important reasons to learn DSA)
Case in point, if you have to list all the employees in an organization with their respective positions in mind, you can do so easily using the principle of a tree data structure. It’ll define the hierarchy of employees and make it easy for others to reach out to specific individuals.
Just look around and you’ll find innumerable examples of various data structures and algorithms in play.
If you want to clarify the concept of data structures and algorithms from scratch, refer to this article.
The full-stack developer course at Masai has a focused approach to solving DSA problems on a daily basis. If you're serious about building a scalable career in the tech industry as a developer, do check out the part-time and full-time courses here.
Happy Coding!
FAQs
What does a tree structure in programming mean?
A tree is a common data structure in computer science that replicates a hierarchical tree structure. It has a root value and subtrees of children with a parent node, and it is represented as a collection of connected nodes.
Is the tree data structure challenging to learn?
No, the tree data structure is not challenging. Understanding the connections between nodes, which can be challenging to determine, is the major problem with trees. However, if you get how a tree is made, working with one becomes rather simple.

