Linked List in Data Structures - Explained with Examples
You must have played those treasure hunt games where you have to solve a puzzle to get the clue that directs you to the next steps in the hunt and so on. A linked list works in a similar fashion.

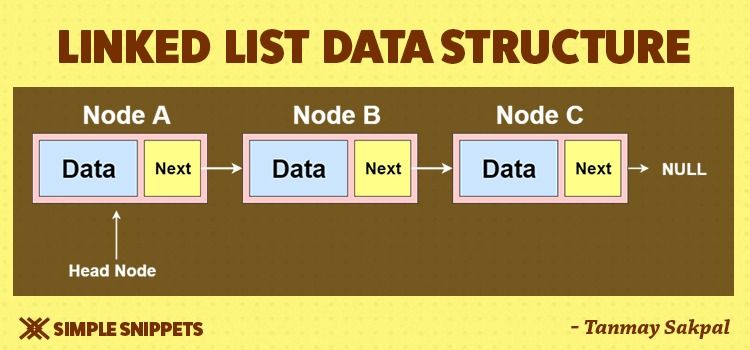
A linked list is a type of data structure in which elements are connected to each other through links or pointers. Each element (called a node) has two parts - the data and a link pointing to the next node.
Definition: A linked list is a type of linear data structure that occurs when the data elements do not reside in consecutive memory regions. A linked list's components are connected using pointers (entities that lead to the next member).
A linked list comprises of nodes, each of which has an information field and a reference (link) to the subsequent node in that list.
Okay! So, it’s highly likely that many of you didn’t get that. And we don’t want that. Our aim is to put it out in a layman's way so even beginners could understand what exactly is a linked list.
Well, at this point, many of you are quite likely to have not understood this. That is something we do not desire. Our goal is to explain it in simple language so that even novices may comprehend what a linked list is.
So, let’s break it down -
“A type of data structure”
What is a data structure?
A data structure is how we store and organize data so we can perform different operations on it easily.
Does it have types?
Yes, data structures are of different types depending on what form we need the data to be stored in, and how we perform any operation on it.
A linked list stores data in a linear sequence (How data is stored) using pointers, and these pointers allow us to add or remove elements without restructuring the whole thing (how are we operating on it).
Table of Contents
Data structures and algorithms
Representation of linked lists
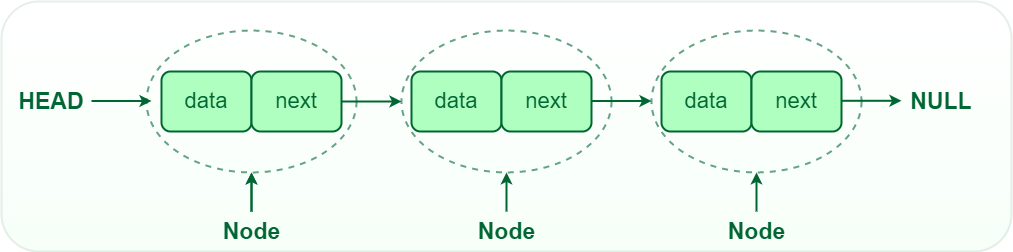
An array is one similar data structure that has elements in a linear order, the only difference being - the array uses indices to assign positions while a linked list uses links that point to the next element/node. (Yes! We will understand the difference in detail later).
Here’s a better way to understand a linked list-
Think of a train! It has numerous bogies connected to each other. If we have to add a new bogie X somewhere in the middle of two bogies, say L and R, we can simply disconnect L and R and add the new one in the middle. Now L will be connected to X, and X will be connected to R.
This kind of insertion wouldn’t be possible in an array-like setup where you’d have to shift all bogies to make space for a new one.
You must have played those treasure hunt games where you have to solve a puzzle to get the clue that directs you to the next steps in the hunt and so on.
A linked list works in a similar fashion where a node has the reference link to the next node in the list.
Why do we need linked lists?
We need linked lists for the various advantages listed below,
- A linked list is a linear data structure that dynamically stores a group of data segments.
- These data segments are represented by nodes, which are connected by links or pointers.
- Each node has information stored in a linked list and a reference to the location of its subsequent node.
- The final node has null in its second field to avoid it will be pointing to no node
- A linked list's size can be increased or decreased as needed.
- It does not take up much memory space.
The question is fairly simple - If we have a linear data structure in arrays, why do we even need linked lists?
Because, in an array, it’s much more difficult to insert or add an element. Even in a dynamic array, all the other elements would have to shift in order to make space if we have to add an element at the start of the index.
Also, there is a possibility that you’d need to allocate more memory space to the array before inserting an element.
This is where linked lists find their significance-
Remember, a linked list maintains its order using pointers, which allows us to insert or remove nodes at random positions with ease.
Since the position of a node is stored in the pointer of the previous node, the nodes don’t necessarily have to be consecutive. They can be stored anywhere in memory and still be connected through the links.
Representation of linked lists
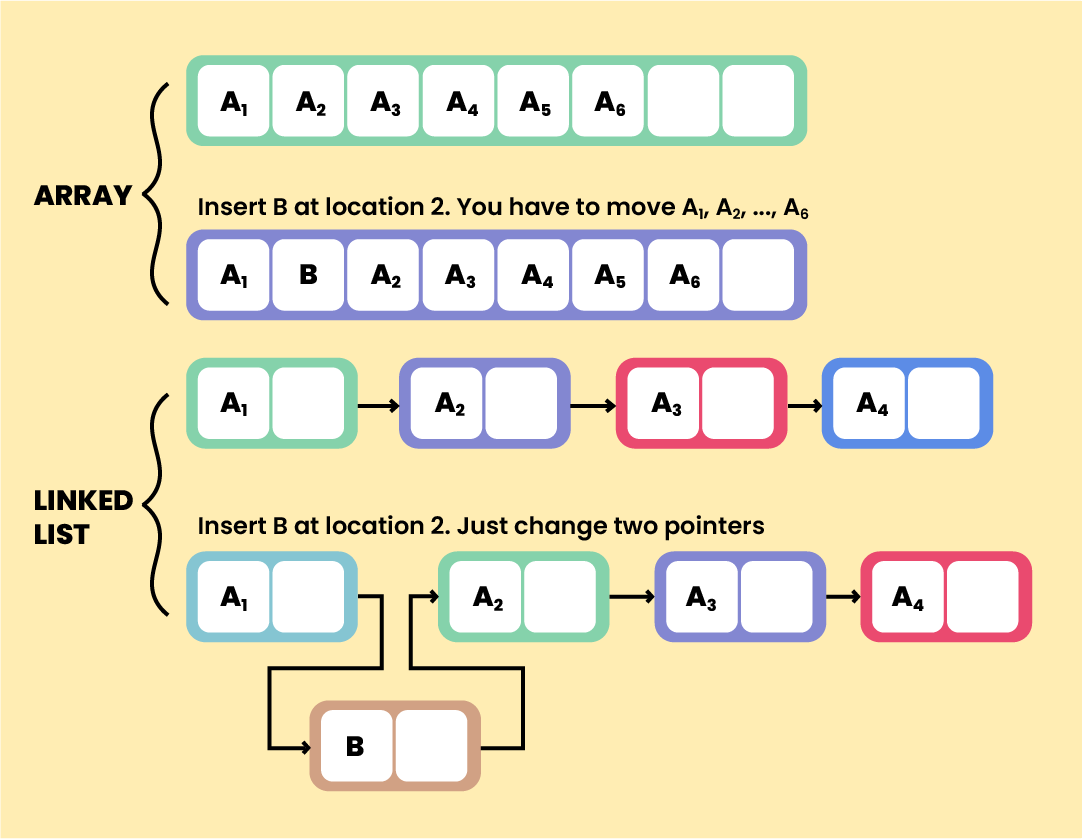
We can visualize a linked list as a chain of nodes; where every node contains a data field and a reference link to the next node in the list.
The first node in the sequence is termed as ‘head’. And we can identify the last node as the one which points to ‘Null’.
Each node consists of -
- A data field
- Reference to the next node
Structure of a node in C language-
struct node
{
int data;
struct node *next;
};Let’s make a simple linked list with three items to understand this better.
/* Initialize nodes */
struct node *head;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;
/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));
/* Assign data values */
one->data = 1;
two->data = 2;
three->data=3;
/* Connect nodes */
one->next = two;
two->next = three;
three->next = NULL;
/* Save address of first node in head */
head = one;Here's how it'll look-
Operations in a linked list
Following are the various operations to perform the required action on a linked list:
- Traversal - To access each element of the linked list.
- Insertion - To add/insert a new node to the list.
- Deletion - To remove ane existing node from the list.
- Search - To find a node in the list.
- Sort - To sort the nodes.
Now, let’s look at each of these operations separately-
Insertion
It’s more than a one-step activity. First, we create a node with the same structure and specify the location where we’ll insert it.
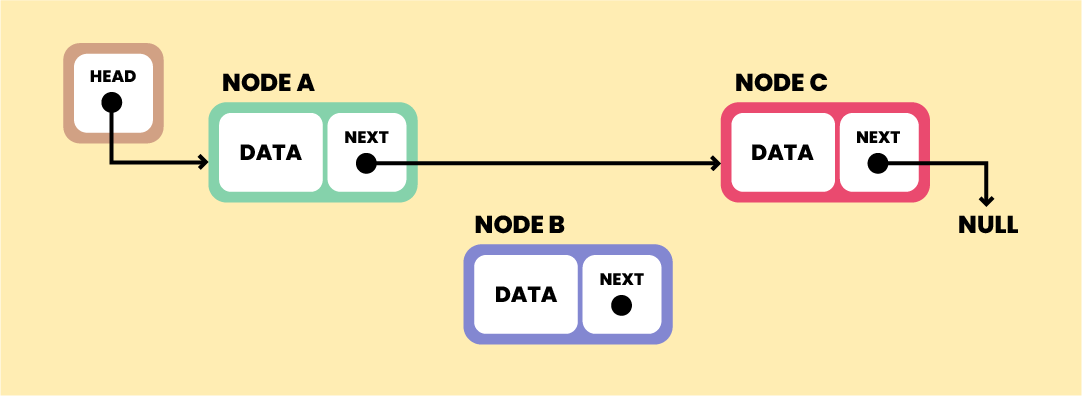
Suppose, we have to insert Node B between the two nodes A and C.
The new Node B will point to Node C.
NodeB.next - Node C
Now, Node A should point to Node B
NodeA.next — NodeB
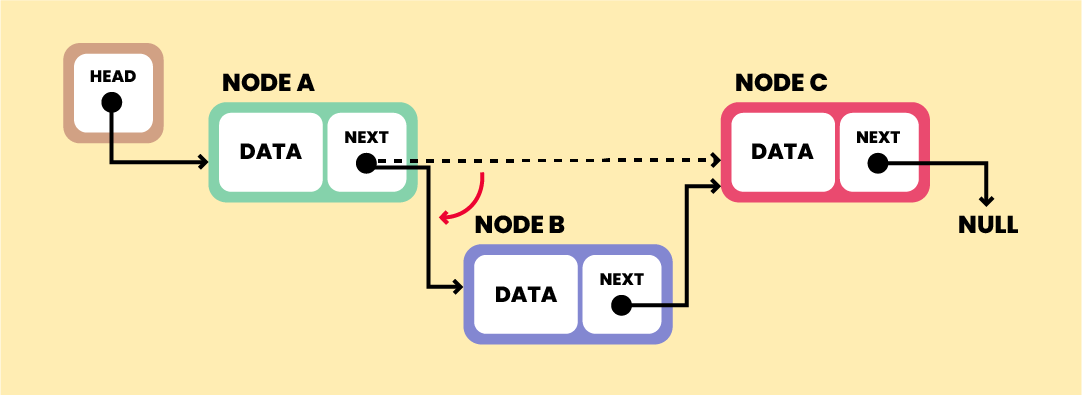
Doing this will place the new node in the middle of the two nodes; as we wanted.
If we have to insert a node at the beginning of the list; the new node should point to the Head (First).
Similarly, if we have to insert a node at the end; the last node should be made to point to the new node, and the new node should be pointing to ‘Null’.
Deletion
Just like insertion, deletion is also a multi-step process.
First, we track the node to be removed, by using searching algorithms.
Once, it’s located, we’ll change the reference link of the previous node to the node that is next to our target node.
In this case, Node A will now point to Node C.
NodeA.next - NodeC
Once, the link pointing to the target node is removed, we'll also remove the link from Node B to Node C.
Now, Node B should point to ‘Null’.
Node B.next — Null
Now we can either keep it in memory or deallocate memory and eliminate Node B.
To delete a node from the beginning, we’ll simply direct the ‘head’ to the second node in the list.
In case of deleting the last node, the second last element will be directed to point to Null.
Search
We search for a node on a linked list using a loop. Suppose, we have to find Node X on a list.
- First, we’ll assign the ‘Head’ as the ‘Current’ node.
- Then, we’ll use a loop until the ‘Current’ node is ‘Null’ since the last element points to ‘Null’.
- In each repetition, we’ll check if the key of the node is equal to ‘Node X’. If the key matches this item, return true, else return false.
// A Generic Node class is used to create a Linked List
class Node<E> {
// Data Stored in each Node of the Linked List
E data;
// Pointer to the next node in the Linked List
Node<E> next;
// Node class constructor used to initializes the data
// in each Node
Node(E data) { this.data = data; }
}
class LinkedList<E> {
// Points to the head of the Linked
// List i.e the first element
Node<E> head = null;
int size = 0;
// Addition of elements to the tail of the Linked List
public void add(E element)
{
// Checks whether the head is created else creates a
// new one
if (head == null) {
head = new Node<>(element);
size++;
return;
}
// The Node which needs to be added at
// the tail of the Linked List
Node<E> add = new Node<>(element);
// Storing the instance of the
// head pointer
Node<E> temp = head;
// The while loop takes us to the tail of the Linked
// List
while (temp.next != null) {
temp = temp.next;
}
// New Node is added at the tail of
// the Linked List
temp.next = add;
// Size of the Linked List is incremented as
// the elements are added
size++;
}
// Searches the Linked List for the given element and
// returns it's particular index if found else returns
// -1
public int search(E element)
{
if (head == null) {
return -1;
}
int index = 0;
Node<E> temp = head;
// While loop is used to search the entire Linked
// List starting from the tail
while (temp != null) {
// Returns the index of that particular element,
// if found.
if (temp.data == element) {
return index;
}
// Gradually increases index while
// traversing through the Linked List
index++;
temp = temp.next;
}
// Returns -1 if the element is not found
return -1;
}
}
public class GFG {
public static void main(String[] args) throws Exception
{
// Initializing the Linked List
LinkedList<Integer> ll = new LinkedList<>();
// Adding elements to the Linked List
ll.add(1);
ll.add(10);
ll.add(12);
ll.add(-1);
ll.add(0);
ll.add(-19);
ll.add(34);
// Element to be searched
int element = -1;
// Searching the Linked
// List for the element
int ans = ll.search(-1);
if (ans == -1) {
System.out.println(
"Element not found in the Linked List");
}
else
System.out.println(
"Element found in the Linked List at "
+ ans);
}
}
Output: Element found in the linked list at 3.
Sort
To sort elements in ascending order, we’ll use Bubble Sort. This is how-
- Assign ‘Head’ as the ‘Current’ node and create another node index for later use.
- If ‘Head’ is null, return
- Otherwise, we’ll run a loop until it becomes null.
- In each iteration, we’ll store the next node of ‘Current’ in the index.
- We’ll then check if the data of the current node is greater than the next node. In case, it is greater, we’ll swap ‘Current’ and ‘Index’. We’ll follow the same process throughout.
Let’s say we have to sort the numbers - 7, 5, 4, and 6 in ascending order;
Here’s the Java program to do so using bubble sort-
// Java program to sort Linked List using Insertion Sort
public class LinkedlistIS
{
node head;
node sorted;
class node
{
int val;
node next;
public node(int val)
{
this.val = val;
}
}
void push(int val)
{
// allocate node
node newnode = new node(val);
// link the old list off the new node
newnode.next = head;
// move the head to point to the new node
head = newnode;
}
// function to sort a singly linked list using insertion sort
void insertionSort(node headref)
{
// Initialize sorted linked list
sorted = null;
node current = headref;
// Traverse the given linked list and insert every
// node to sorted
while (current != null)
{
// Store next for next iteration
node next = current.next;
// insert current in sorted linked list
sortedInsert(current);
// Update current
current = next;
}
// Update head_ref to point to sorted linked list
head = sorted;
}
// function to insert a new_node in a list. Note that
// this function expects a pointer to head_ref as this
// can modify the head of the input linked list
// (similar to push())
void sortedInsert(node newnode)
{
// Special case for the head end
if (sorted == null || sorted.val >= newnode.val)
{
newnode.next = sorted;
sorted = newnode;
}
else
{
node current = sorted;
// Locate the node before the point of insertion
while (current.next != null && current.next.val < newnode.val)
{
current = current.next;
}
newnode.next = current.next;
current.next = newnode;
}
}
// Function to print linked list
void printlist(node head)
{
while (head != null)
{
System.out.print(head.val + " ");
head = head.next;
}
}
// Driver program to test above functions
public static void main(String[] args)
{
LinkedlistIS list = new LinkedlistIS();
list.push(7);
list.push(5);
list.push(4);
list.push(6);
System.out.println("Linked List before Sorting..");
list.printlist(list.head);
list.insertionSort(list.head);
System.out.println("\nLinkedList After sorting");
list.printlist(list.head);
}
}
Output
Original list : 7 5 4 6
Sorted list : 4 5 6 7
Time complexity : 0 (n^2)
Space complexity : 0 (1)
Types of linked lists
There are 4 key types of linked lists-
Singly linked list
Till now we have talked about singly linked lists. It is the most commonly used linked list containing two parts- the data field, and the reference pointer to the next element.
It is the most basic linked list, with each node containing some data and a reference to the subsequent node of the same data type.
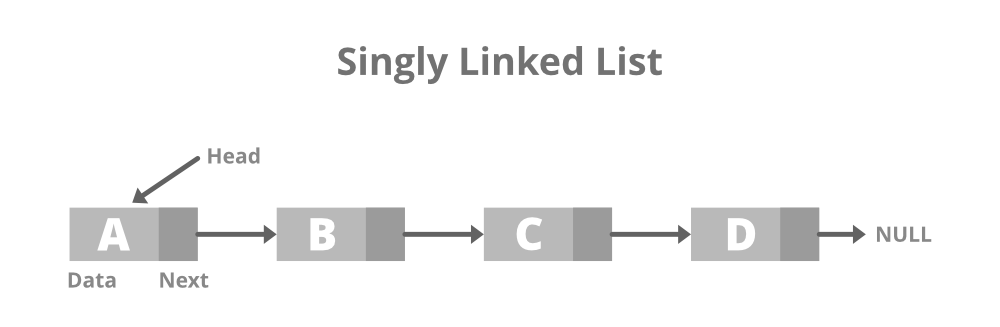
In a singly linked list, only forward traversal is possible; as it has only one pointer that points to the next node. For the same reason, it is also termed a ‘one-way chain’.
Doubly linked list
A doubly linked list contains two pointers- one pointing forward and the other one pointing back to the previous node.
A doubly linked list, also known as a two-way linked list, is an advanced version of linked list that carries a pointer to both the following and earlier nodes in the chain.
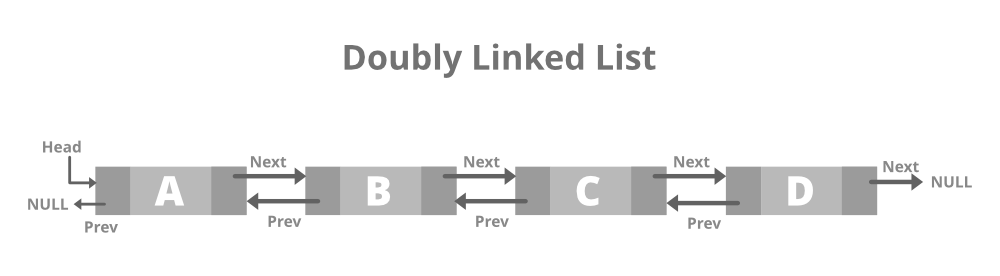
That was simple guessing by the name, wasn’t it?
So in total, a doubly-linked list contains three parts, including, of course, the data part.
Let’s say we have three nodes - 1,2, and 3 with addresses A, B, and C respectively. They will be represented in a doubly-linked list as-
The front node has a ‘Null’ value in the address part which shows the previous node’s address.
A doubly-linked list allows us to traverse in both directions.
Circular linked list
It’s a type of linked list in which the very last node is connected to the first node, thus forming a circular loop.
A circular linked list is one in which the end node carries a pointer to the list's initial node.
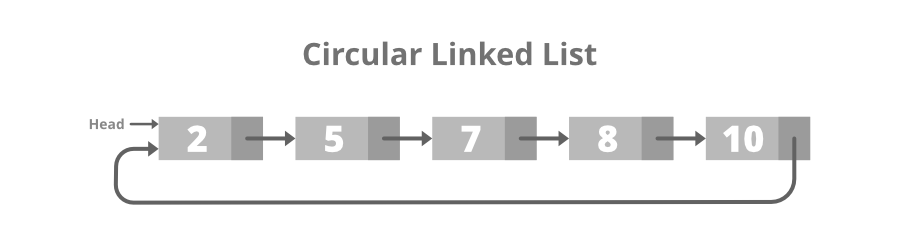
A circular linked list has no starting and ending node, and we can traverse both forward and backward.
Doubly circular linked list
It combines the features of both circular linked lists and doubly linked lists.
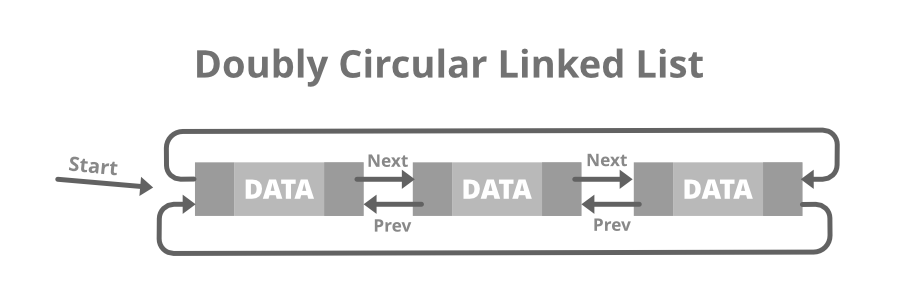
The nodes have two pointers for the next and previous node, and the last node points to the first node making it a circular doubly linked list.
This type of linked list doesn’t have ‘Null’ in any of the nodes. Both the first and the last nodes contain addresses of each other.
A circular doubly linked list makes the search operation twice as efficient, as it offers easy maneuvers of pointers.
Applications of linked lists
In programming
Implementing stacks and queues
Linked lists are used to implement stack and queue data structures. How?
As a stack follows the Last In First Out principle, every PUSH operation will be INSERT_IN_BEGINNING and every POP operation will be DELETE_IN_BEGINNING in the linked list.
And, in the First In First Out structure of a queue, we’ll maintain two pointers - the head pointing to the start of the linked list, and the tail pointing to the end of the linked list. Every PUSH operation will be INSERT_IN_END and every POP operation will be DELETE_IN_BEGINNING.
Implementing graphs
Graphs can also be implemented using the adjacency list representation.
It can be depicted as an array of linked lists where lists store the adjacent vertices.
Polynomial manipulation
A polynomial, in mathematics, is a collection of different terms, comprising coefficients, variables, and exponents. They’re not supported as a data type by most languages. However, linked lists can represent polynomials with ease.
How?
Each polynomial term takes up a node in the linked list. It is also made sure that the terms are arranged in the decreasing order of exponents for better efficiency.
Each node would consist of 3 parts-
Let’s say we have-
4x4+ 11x3 - 2x2 + 1
Here - 4, 11, 2, and 1 are the coefficients while 4,3,2, and 0 are the exponential values respectively.
To represent 4 terms, we’ll need a linked list with 4 nodes.
Representing polynomials this way allows us to perform various mathematical operations easily.
Dynamic memory allocation
As we know that nodes of a linked list are not stored in contiguous memory locations, but instead created dynamically at runtime. So, linked lists can be helpful in dynamic memory allocation where we don't know the exact number of elements we’re going to use.
In real life
Having a significant role in programming, linked lists certainly have many real-life applications. Let's look at a few of them -
In web browsers
While moving through web pages, you have both options available - to either move to the next page or the previous page. This is only possible because of a doubly linked list.
In music players
Similarly, we can switch to the next and the previous song in a music player using links between songs. We can also play songs either from the starting or the end of the playlist.
In image viewer
The next and the previous photos are linked, and we can easily access them by using the previous and next buttons.
In operating systems
The thread scheduler uses a doubly-linked list to maintain the list of all processes running at any time. It enables us to move a certain process from one queue to another with ease.
In Multiplayer games
Online multiplayer games such as the likes of PUBG and Call of Duty use a circular linked list to swap between players in a loop.
Linked list vs Array
Arrays can be considered the default type in almost all programming languages, due to their wide usage.
But there are many use-cases where using arrays isn’t the ideal solution. Like when we don’t know the number of elements to be stored, or when we know that we’d need to do a lot of insertions and deletions later. In such cases, we need an advanced data structure like a linked list. Of course, just like arrays, linked lists have their own limitations too.
With that being said, let’s look at the key differences between an array and a linked list-
Accessing an element
Arrays support random access which means you can access any element directly using their index, like arr[0] for accessing the 1st element, arr[3] for the 4th element, and so on.
Whereas, only sequential access is possible in a linked list; you have to sequentially traverse the entire list up to that element.
Insertion and Deletion
Due to the fixed and consecutive memory locations in an array, insertion and deletion operations take more time.
Meanwhile, new elements can be stored anywhere in the memory of a linked list. We just need to sort the address of memory locations of the previous node, which will then point to the newly added node.
Memory Allocation
Memory is allocated while declaring the array, at compile time. It’s also called static memory allocation.
Whereas, linked lists support dynamic memory allocation. Memory can be allocated at runtime while adding a new node.
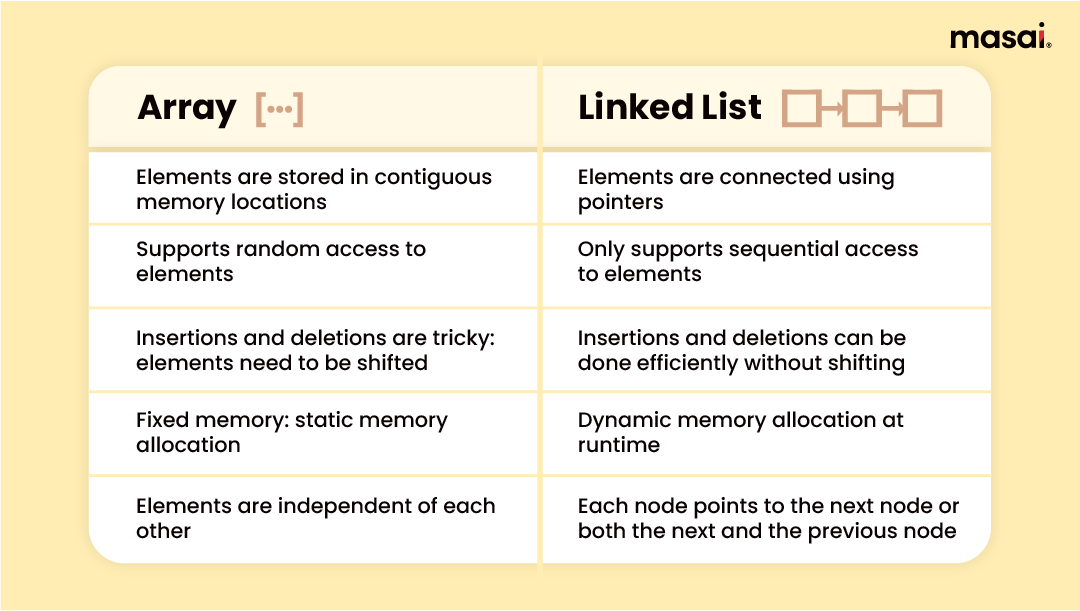
Know the differences between arrays and linked lists in detail here.
Final thoughts
Linked lists are adaptable data structures that allow for flexible allocation of memory as well as effective deletion and insertion operations. Developers or programmers must understand the fundamentals of linked lists as these details will let them employ linked lists to address a variety of issues while also broadening their understanding of information structures and processes.
We hope you got a complete understanding of linked lists and how they work to support the various web applications we use in our day-to-day lives.
If you want to learn data structures and algorithms from scratch, this article would be a great place to start.
If you’re perhaps looking to build a high-growth career in web development or data analytics, do explore these pay-after-placement-based courses by Masai.
Featuring a 9-9-6 (9 AM-9 PM, Monday-Saturday) schedule, industry-level training, employability skill-building sessions, and real-time projects, these programs are a sure-set way to propel your career in the right direction: irrespective of your educational background.
Cheers!
FAQs
What is the number of points necessary to make a short-linked list?
To build a significant linked list, three types of pointers are normally required:
- A "head" pointer: This is employed to navigate to the first item in a list.
- A "tail" pointer: This is used to locate the final node. The final node is important as the next reference to this would be a NULL.
- In each node, a pointer refers to the next node element.
How do linked lists store information?
A linked list is a collection of nodes that are connected together. A linked list is a data structure with a linear form designed to store a collection of things. The linked list may also be used to hold a variety of items that are related.

